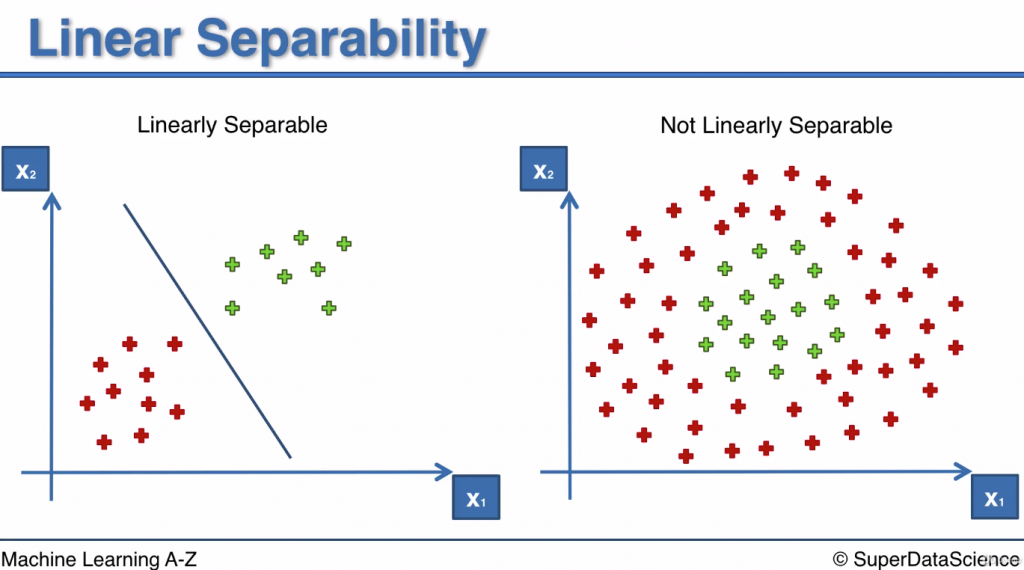
當數據是linearly separable: 傳統的SVM 可以將兩種數據很好的分類
當數據是not linearly separable: 無法在二維空間用單純的直線來將數據做分類
因此需要加上kernel setting 來解決這樣的問題
後面會從三點來講解：

1. 從二維到高維空間的投射
2. 如何用kernel function算出界線
3. 幾種科學家常用的kernel function

從二維到高維空間的投射(A Higher-Dimensional Space)

一維問題

f = x - 5 -> 原先的點在一維線上, 難以用直線切開
f = (x-5)^2 -> 將這些點投射到二維平面上, 就可以用一條直線將點切分開來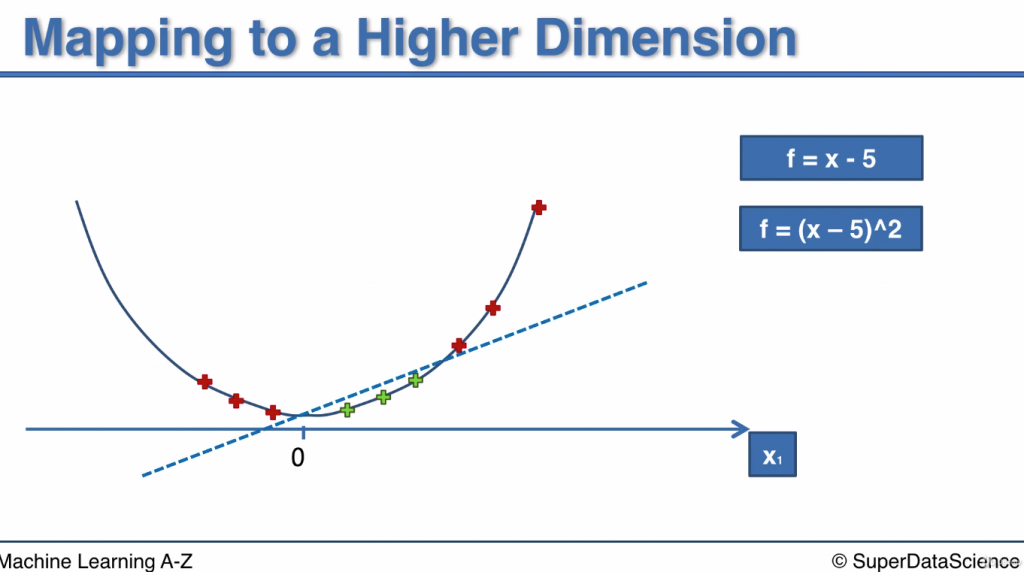

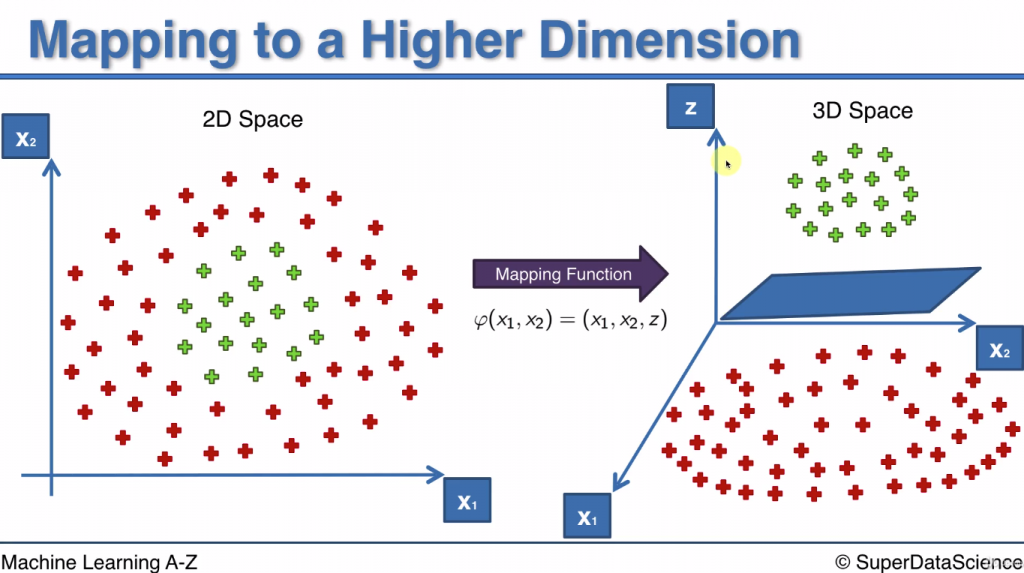
二維問題

現在問題變成二維的, 我們一樣將所有的點(x,y)座標增加z座標, 代表投影成三維空間中的點
這時候就可以用一個超平面(Hyperplane)將兩邊點切分開了
這邊忽略z 的算法, 只要知道z和x1,x2一定有關係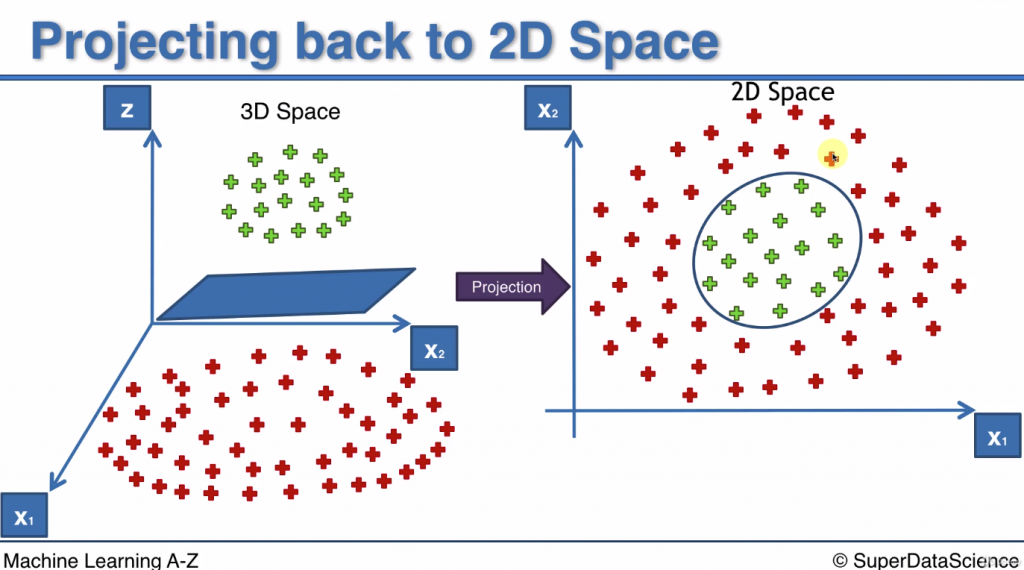

接著再將三維空間的超平面做投影, 降維到二維空間上, 剛剛的超平面就會變成一個圓
這個圓就是ＳＶＭ分類邊界

compute-intensive

然而從計算角度來說非常耗時間, 因此需要引用kernel function可以避免繁瑣的計算並達到從高維->低維->高維的效果